As illustrated in Figure the points

 

 

         

 

  

 

 

 

 

 

 

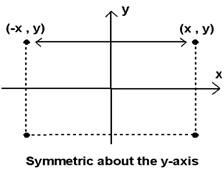
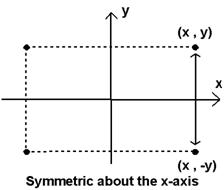
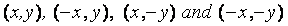
form the corners of a rectangle

For obvious reasons, the points (x,y) and (x,-y)

 

are said to be symmetric about

the x-axis and the points ( x, y) and ( -x, y) are symmetric about the y-axis  and the points (x, y) and ( -x, -y) symmetric about the

 

SYMMETRY AS A TOOL FOR GRAPHING

 By taking advantage of symmetries when they exist, the work required to obtain a graph can be reduced considerably.

Example#9

Sketch the graph of the equation    

Solution:-

The graph is symmetric about the y-axis since substituting 

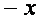
for x yields

which simplifies to the original equation

As a consequence of this symmetry, we need only calculate points on the graph that lies in the right half of the xy-plane ( x    0).    

The corresponding points in the left half of the xy-plane ( x   0)

can be obtained with no additional computation by using the symmetry. So 

put only positive x-values in given equation and evaluate corresponding y-values.

Since graph is symmetric about y-axis, we will just put negative signs with the x-values taken before and take the same y-values as evaluated before for positive x-values.

 

 

   

 

 

Example#10

Sketch the graph of the equation     

Solution:-

 

If we solve 

for y in terms of x, we obtain two solutions,

The graph of

is the portion of the curve

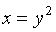
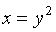
that lies above or touches the x-axis

(since    ),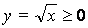

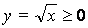and the graph of

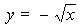
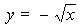
is the portion that lies below or touches the x-axis (since

However, the curve

is symmetric about the x-axis because substituting -y for y yields

 

 

which is equivalent to the original equation.

 

Thus, we need only graph

and then reflect it about the x-axis to complete the graph

 

 

 

 

 

 

 

 

 

 is the  graph of the function.

 

 

 

 

 

 

 

 

is the required graph of the function.