Rectangular Coordinate System
So here is another terminology. The COORDINATE PLANE and the
ordered pairs we just discussed is together known as the
RECTANGULAR COORDINATE SYSTEM.
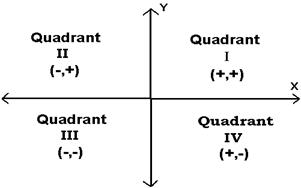
In a rectangular coordinate system the coordinate axes
divide the plane into four regions called quadrants.
These are numbered counter clockwise with Roman
numerals as shown in the Figure below.
As
illustrated in Figure it is easy to determine the
quadrant in which a given point lies from the signs
of its coordinates: a point with two positive
coordinates ( + , + ) lies in Quadrant I, a point
with a negative x-coordinate and a positive
y-coordinate 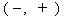 lies in Quadrant II, and so forth
lies in Quadrant II, and so forth
Points with a zero x-coordinate lie on the
y-axis and points with a zero y-coordinate lie
on the x-axis.
Now
remember that the idea of having a number line
and that of a rectangular coordinate systems was
to describe algebraic statements geometrically
and vice versa?? Well, what are these algebraic
statements?? They are equations and
inequalities. Let's look at the equations and
how we can express them GEAOMETRICALLY using the
XY-PLANE
Suppose
we have the equation
We
define a SOLUTION of such an equation to be an
ordered pair of real numbers (a, b) such that the
equation is satisfied when we substitute x = a and y
= b. The SET OF ALL SOLUTIONS IS CALLED THE SOLUTION
SET OF THE EQUATION. Here are some examples
Example#1
The pair
(3,2) is a solution of
6x-4y=10
since this equation is satisfied when we
substitute x = 3 and y = 2. That is
6(3)-4(2)=10
which is true!!
However, the pair (2,0) is not a solution, since
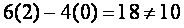
We
make the following definition in order to start
seeing algebraic objects
geometrically.
Previous
TOC
Next