Each line is a line with numbers on it, so to
define a point in the PLANE, we just read of the corresponding
points on each line. For example I pick a point in the plane
Then I draw
a line from the horizontal line all the way to P, and I
draw another line from the vertical line to the point P.
Now I measure the lengths of these lines, which is in
essence the same as measuring the distance UP to the
point P from the horizontal line, and the distance to
the RIGHT from the vertical line. We know how to do that
by now!! Say the distance to the right is 4 units (the
units could be anything, m, cm, mm), and 3 units UP. SO
the point is defined by the COORDINATE (4,3) in the
PLANE!!! We will write this as P(4,3) to denote that P
is the point with coordinate (4,3)
But what is
(4,3)?? Is it different than (3,4)?? Sure looks like the
interval from 4 to 3 !!! Well Let's put it formally.
By an
ordered pair of real numbers we mean two real numbers in
an assigned order. Thus, there is a "first number" and a
,” second number”. The symbol ( a, b) is used to denote
the ordered pair of real numbers in which a is the first
number and b is the second number. Because order
matters, the ordered pairs (4, 3) and (3,4) are regarded
to be different. AND, although the interval from 4 to 3
is written as (4,3) as well, the CONTEXT of the
discussion will make it clear whether the interval is
being discussed or the ordered pair. This is
unfortunately the case in most of math, since if we
didn’t repeat most of the notation, then just the
notation will be hard to handle, let alone the
concepts!!!
You must be
wondering why we took the vertical line as a point of
reference to count units to the right, and the
horizontal line to count units up??? Well, the reason is
that I want to have a point of reference. Just like on
the real number line where we had the 0 as the ORIGIN,
similarly, in this case we will take the COORDINATE or
the POINT (0,0) as our reference or the ORIGIN.
Notice that
when I measured the units UP and DOWN in the above
example, I was actually measuring from the point (0,0).
Convince yourself of this.
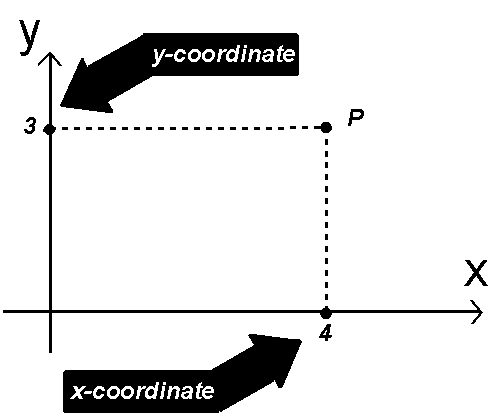
It is hard
to keep saying vertical line and horizontal line. So we
introduce terminology here. You may have heard this
before. We will call the Vertical line the Y-AXIS, and
the Horizontal line the X-AXIS. Then in the POINT
(4,3), 4 will be called the X-COORDINATE, and 3 will be
called the Y-COORDINATE. Sometimes we will say x=4, y=3,
for short.
BUT HERE
IS AN IMPORTANT QUESTION???? We saw how to assign
ordered pairs to the points in the plane. Is this a
one-to-one assignment?? That is, are we sure that we
won’t get the same ordered pair assigned to a different
point in the plane.
BUT
HERE IS AN IMPORTANT QUESTION???? We saw how to
assign ordered pairs to the points in the plane.
Is this a one-to-one assignment?? That is, are
we sure that we won’t get the same ordered pair
assigned to a different point in the plane.
Well
we are sure that we WON’T. The reason is the way
we draw perpendicular lines from the coordinate
lines to the POINT. The intersection of any such
two perpendicular lines has to be a unique
point!!!!! Conversely, if we start with an
ordered pair of real numbers (a, b) and
construct lines perpendicular to the x-axis and
y-axis that pass through the points with
coordinates a and b, respectively, then these
lines intersect at a unique point P in the plane
whose coordinates are (a, b). Thus, we have a
one-to-one correspondence between ordered pairs
of real numbers and points in a coordinate
plane. I don’t think you need a long discussion
about this, its fairly straight forward.
To
plot a point P(a, b) (Remember that this means
the point P with coordinates (a,b) ) means to
locate the point with coordinates (a, b) in a
coordinate plane. For example, In the figure
below we have plotted the points P(2,5),
Q(-4,3), R(-5,-2), and S(4,-3).Now this idea
will enable us to visualise algebraic equations
as geometric curves and, conversely, to
represent geometric curves by algebraic
equations. Remember we said this in the first
lecture!?? This is in essence what the famous
French mathematician Descartes developed.
|
